Článek popisuje pokročilou metodu navrhování ocelových prvků pod obecným zatížením, včetně styčníků a navazujících prutů. Přístup je založený na metodě konečných prvků s komponentami CBFEM. Numerický model je verifikován citlivostními studiemi tlačených sloupů a ohýbaných nosníku. Model je dále validován na sadě vzorků tlačených symetrických úhelníků se šroubovanými styčníky.
Pruty ocelových konstrukcí se tradičně navrhují izolovaně, kontext celé konstrukce je při jejich posouzení zohledněn pouze uvážením vhodných okrajových podmínek. Takový přístup je dostačující pro ideální uložení a přímé pruty namáhané specifickou kombinací vnitřních sil. Tento článek popisuje komplexnější přístup k návrhu – prut je modelován společně s přípoji a navazujícími prvky. Tuhost styčníků a vliv navazujících prutů na únosnost analyzovaného prutu je tak v analýze zohledněn přímo.
ANALÝZA KONSTRUKCE JAKO CELKU
Statický návrh typicky začíná u 3D prutového modelu konstrukce. Do prutového modelu konstrukce jsou vneseny globální imperfekce a je provedena pružná, geometricky nelineární analýza. Tuhost styčníků bývá běžně zjednodušena na kloubové nebo tuhé uložení. Výsledkem jsou vnitřní síly a deformace. Většina návrhových softwarů pak umožňuje posudky běžných prutů. Problém nastává s nestandardními pruty, jako například zakřivené a prolamované, s náběhy, případně prvky zatížené kombinací vnitřních sil, kterou normové posudky nepokrývají, například kroucení společně s ohybovými momenty. Takové pruty nezbývá než navrhnout aproximací, nebo pokročilými metodami. Možným řešením je CBFEM analýza celých částí konstrukce.
CBFEM PRO NÁVRH PRVKŮ
Metoda konečných prvků s komponentami CBFEM využívá poznatků metody komponent [1] používané pro návrh styčníků. Síly jsou ale na jednotlivé komponenty rozneseny metodou konečných prvků, což umožňuje návrh obecné geometrie a zatížení. Zároveň jsou tyto modely relativně jednoduché a jejich řešení je rychlé. Do CBFEM byla nedávno implementována analýza velkých deformací, což otevřelo cestu k návrhu celých výseků konstrukce – prutů se styčníky. Plechy jsou modelovány deskostěnovými konečnými prvky, únosnost materiálu s bilineárním materiálovým diagramem je daná von Misesovou podmínkou na návrhové mezi kluzu. Sklon plastické větve je E/1 000, zpevnění vlivem plasticity je tedy zanedbatelné. Plastické přetvoření je omezeno 5 %. Pro modelování šroubů a svarů se využívají nelineární pružiny s interpolačními vazbami, které byly kalibrovány, aby odpovídaly normovým únosnostem a tuhostem.
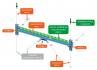
Analyzovaný prut je modelován deskostěnovými prvky, stejně jako přiléhající části navazujících prutů. Oblasti v okolí styčníků jsou tedy modelovány velmi přesně a zachycují reálné uložení prutu v konstrukci. Zbývající části navazujících prutů jsou nahrazeny 1D prvky, což zvyšuje rychlost výpočtu – viz obr. 1. Analyzovaný prut může být zatížen přímo, nebo přes navazující pruty a styčníky.
Návrh probíhá ve třech krocích. Nejdříve je provedena materiálově nelineární analýza (MNA). Tato analýza není dostatečná pro zohlednění problémů stability, ale ověří se správnost modelu a zadání zatížení. Dále se provede lineární bifurkační analýza (LBA), pomocí které získáme tvary vybočení konstrukce a součinitele kritického zatížení. Často je rozhodující první tvar vybočení, což ale není pravidlem. Do dalšího postupu by měly být zohledněny všechny výsledné tvary vybočení a jejich vliv na únosnost. Nakonec je provedena geometricky nelineární analýza s imperfekcemi (GMNIA). Imperfekce jsou do modelu zavedeny úpravou sítě konečných prvků, a to podle zvoleného tvaru (nebo kombinace tvarů) vybočení a zadaných amplitud. MNA je dostatečná pouze v případě, že stabilita nerozhoduje o únosnosti modelu, čili když kritický součinitel zatížení je αcr > 10. V ostatních případech je nezbytná analýza GMNIA se dvěma kritérii únosnosti:
- Plastické přetvoření εpl < 5 %
- Konec konvergence modelu
GMNIA pro hledání řešení využívá iterační Newton-Raphsonovu metodu. Model je zatěžován přírůstky sil a výpočet končí, když není možné zatížení dále navyšovat.
IMPERFEKCE
Pro zavedení imperfekcí existuje několik přístupů. Nejpřesnějším způsobem je modelování reziduálních napětí, společně s geometrickou imperfekcí. Pro nejběžnější průřezy existují modely rozdělní reziduálních napětí, ale přivaření výztuhy nebo náběhu tato rozdělení naruší, a to často přímo v rozhodujícím místě – pod koncentrovaným zatížením, případně ve styčnících. EN 1993-1-1 [2] nahrazuje všechny imperfekce jednou ekvivalentní geometrickou imperfekcí. Její amplitudu pro každou ze vzpěrných křivek uvádí v Tabulce 5.1. Alternativně je možné imperfekce získat z Článku 5.3.2 této normy, pomocí vzorců odvozených z teorie druhého řádu. Třetím přístupem je postup dle návrhu nové generace Eurokódů [3], kde byl způsob stanovení počátečních imperfekcí přepracován.
VERIFIKACE A VALIDACE MODELU
Verifikace je srovnání modelu s jinou ověřenou metodou. CBFEM model byl verifikován na příkladech tlačených sloupů, ohýbaných nosníků, prolamovaného nosníku a nosníku s náběhy, a to s ideálními okrajovými podmínkami, aby bylo možné srovnání s analytickými metodami. Byl také sledován vliv modelování průřezů, kdy v CBFEM nejsou zohledněna zaoblení mezi stojinou a pásnicemi válcovaných průřezů – viz obr. 2.
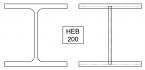
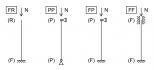
Bylo analyzováno 24 variant tlačeného sloupu. Ověřen byl vzpěr okolo tuhé osy y i měkké osy z. Všechny sloupy sdílí stejný průřez HEB 200 a stejnou třídu oceli S 355. Vyšetřován byl vliv 4 různých způsobů uložení – viz obr. 3.
Délka sloupů byla volená tak, aby bylo dosaženo poměrných štíhlostí 0,5; 1,0 a 1,5.
Imperfekce tlačených sloupů byly určeny podle tří přístupů:
- A. EN 1993-1-1:2005, Tabulka 5.1 [2]
- B. PrEN 1993-1-1:2020, second draft, Článek 5.3.3.1 [3]
- C. EN 1993-1-1:2005, Článek 5.3.2 (11) [2]
Pro verifikaci metody na ohýbaných nosnících bylo kromě analytických výsledků využito i numerických výsledků ze softwaru ANSYS, publikovaných v diplomové práci [4]. Nosníky byly zatíženy ohybovým momentem, osamělým břemenem uprostřed rozpětí nebo spojitým příčným zatížením – viz obr. 4.
Pro výpočet počáteční imperfekce ohýbaných nosníků byly uváženy 4 postupy, dále označeny A, B, C a D. První tři uvažují s počáteční imperfekcí pro vzpěr kolem měkké osy, sníženou součinitelem k = 0,5 podle EN 1993-1-1, Článek 5.3.4 (3) [2]. Počáteční imperfekce dle přístupu D je stanovena přímo pro selhání v ohybu s klopením.
- A. EN 1993-1-1:2005, Tabulka 5.1 [2]
- B. PrEN 1993-1-1:2020, second draft, Článek 5.3.3.1 [3]
- C. EN 1993-1-1:2005, Článek 5.3.2 (11) [2]
- D. Dle Snijder et al. [5]
Dále bylo ověřeno chování prolamovaného nosníku z průřezu IPE 300 s třídou oceli S 235, s délkou 6,0 m, výškou 440 mm a 21 rovnoměrně rozmístěnými šestiúhelníkovými otvory – viz obr. 5. Nosník byl prostě podepřený na úrovni dolní pásnice a zatížen spojitým svislým zatížením na horní pásnici.
Pro příklad nosníku s oboustrannými náběhy byl uvažován průřez IPE 270 s třídou oceli S 355. Nosník byl na obou stranách vetknutý, zatížení bylo aplikováno ve střednici prismatického prutu.
Pro validaci modelu je provedeno srovnání s experimenty na vzorcích tlačených ocelových úhelníků se šroubovanými styčníky [6]. U tohoto příkladu nelze stanovit okrajové podmínky a výsledky numerického modelu srovnat s výpočtem. Výsledky GMNIA v CBFEM jsou porovnány s experimenty a FEM modelem. Amplituda počáteční imperfekce byla stanovena dle [7] jako L/300, kde L je délka úhelníku.
VÝSLEDKY
Únosnosti tlačených sloupů z GMNIA jsou porovnány s výpočtem podle EN 1993-1-1 [2] pro skutečný tvar průřezu (EN) a zjednodušený tvar průřezu (ENw) na obr. 6 a 7. Vliv zjednodušení průřezu při modelování je velmi malý, do 2 %. Hodnota počáteční imperfekce je naopak zásadní. Postup (A) dává výsledky na stranu bezpečnou, únosnosti jsou o 8 – 18 % nižší než výsledky analytického výpočtu pro skutečný tvar průřezu. Postup (B) dává výsledky až o 10 – 26 % nižší než EN. Postup (C) je velmi blízko výpočtu dle EN. Rozdíly jsou mezi 6 % na stranu bezpečnou a 1 % na stranu nebezpečnou.
Únosnosti ohýbaných nosníků z GMNIA jsou na obr. 8 také porovnány s výpočtem dle EN 1993-1-1 [2] pro skutečný a zjednodušený tvar průřezu. Pro selhání klopením je vliv modelování průřezu vyšší než pro selhání vzpěrem. Výsledky jsou konzervativní až o 6 %, chybějící zaoblení mají za následek nižší torzní tuhost nosníku. Vliv počáteční imperfekce je však opět rozhodující. Kromě výsledků CBFEM pro čtyři přístupy (A–D) jsou pro přístup C uvedeny i hodnoty z numerického řešení v ANSYS. Pokud porovnáme výsledky obou numerických modelů – CBFEM a ANSYS – dle metody C, je patrná dobrá shoda obou řešení.
Hodnoty počátečních imperfekcí dle přístupů A a B jsou pro uvažované příklady shodné, výsledné únosnosti jsou o 10 – 30 % nižší v porovnání s analytickým řešením dle EN. Imperfekce dle metod C a D vedou k mírně konzervativním výsledkům, rozdíl je do 10 % v porovnání s analytickým řešením pro reálný průřez (EN). Jsou ale velmi přesné vzhledem k očekávané hodnotě vypočtené analyticky pro průřez bez zaoblení (ENw).
Pro příklad prolamovaného nosníku je pružný kritický moment z LBA srovnán s analytickým řešením dle návrhu Eurokódu pro nosníky s velkými otvory ve stojině [8]. GMNIA analýza je pak provedena pro první tvar vybočení s imperfekcí 7 mm, což odpovídá vzpěrné křivce c. Únosnost je porovnána s analytickým výpočtem. Dobrá shoda mezi CBFEM modelem a analytickým řešením je patrná z tabulky 1.
Tabulka 1 – Srovnání pružných kritických momentů a únosností prolamovaného nosníku
| Mcr,an [kNm] |
Mcr,CBFEM [kNm] |
MR,an [kNm] |
MR,CBFEM [kNm] |
|
| IPE 300 | 79 | 78 | 64 | 68 |
Dobré výsledky sledujeme i pro nosníky s náběhy. Uvažované počáteční imperfekce byly 35 mm pro vzpěr na tuhou osu, 12 mm pro vzpěr na měkkou osu a 6 mm pro klopení.
Z tabulek 2 a 3 je patrné, že kritické síly i únosnosti jsou v dobré shodě s tradičními návrhovými metodami.
Tabulka 2 – Srovnání pružných kritických sil a únosností pro vzpěrný tlak
| Ncr,FEM [kN] |
Ncr,CBFEM [kN] |
NR,an [kN] |
NR,CBFEM [kN] |
|
| IPE 270 (y-y) |
2 880 | 2 768 | 1 337 | 1 325 |
| IPE 270 (z-z) |
1 161 | 1 130 | 793 | 789 |
Pro ohyb s klopením je rozhodující průřez v podpoře, v analytickém výpočtu je uvažován ekvivalentní svařovaný průřez s plastickým modulem průřezu a křivka klopení c.
Tabulka 3 – Srovnání pružného kritického momentu a únosnosti v ohybu s klopením
| Mcr,FEM [kNm] |
Mcr,CBFEM [kN] |
MR,an [kNm] |
MR,CBFEM [kNm] |
|
| IPE 270 (LTB) |
375 | 335 | 250 | 240 |
Závěrem jsou uvedeny výsledky z validace pro tlačené šroubované úhelníky – viz obr. 10. Hodnoty únosnosti určené experimentálně a FEM jsou převzaty z [6].
GMNIA s metodou CBFEM poskytuje výsledky, které jsou experimentálním hodnotám u většiny vzorků dokonce blíže než výzkumný FEM model – viz obr. 11.
ZÁVĚR
Byla představena metoda návrhu ocelových prvků, kterou lze v inženýrské praxi efektivně uplatnit při posuzování nestandardních prvků, a to nejen z hlediska jejich geometrie, ale i zatížení, či způsobu připojení na navazující prvky konstrukce.
Metoda byla verifikována na sadě tlačených sloupů, ohýbaných nosníků, nosnících s náběhy a prolamovaném nosníku. Výsledky metody jsou velmi blízko očekávaným analyticky stanoveným hodnotám. Jsou objasněny zdroje odchylek, zejména způsob modelování průřezů v CBFEM a tím i nižší torzní tuhosti válcovaných průřezů. Výsledky GMNIA závisí na vnesených počátečních imperfekcích, je proto srovnáno několik možných přístupů jejich stanovení. Jednodušší přístupy mají za následek konzervativní výsledky, pracnější postupy jsou přesnější. Všechny modely pro verifikaci mají jasné okrajové podmínky a únosnost prutů lze poměrně snadno stanovit běžnými návrhovými postupy.
Výhodnost metody modelování prutu společně s jeho styčníky se ukáže až u složitějších případů. Schopnost metody CBFEM přesně simulovat chování ocelových prvků včetně jejich styčníků je prokázána na příkladech tlačených šroubovaných úhelníků.
Článek byl vytvořen v rámci řešení projektu č. FW01010392 podporovaného Technologickou agenturou České republiky.
Ing. Vojtěch Chalupa
Ing. Martin Vild, Ph.D.
Ing. Lubomír Šabatka, CSc.
Ing. Jaromír Kabeláč, Ph.D.
IDEA StatiCa s. r. o.
prof. Ing. František Wald, CSc.
prof. Ing. Josef Macháček, DrSc.
ČVUT v Praze, Stavební fakulta
REFERENCE:
[1] EN 1993-1-8:2005: Eurocode 3: Design of steel structures – Part 1-8: Design of joints, CEN, 2005.
[2] EN 1993-1-1:2005: Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings, CEN, 2005.
[3] prEN 1993-1-1:2020: Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings, draft, CEN, 2020.
[4] van der Aa, R.P. Numerical assessment of the design imperfections for steel beam lateral torsional buckling, Master thesis, report 2015.96, Eindhoven University of Technology, Eindhoven, Dept. of the Built Environment, Structural Design, The Netherlands, 2015.
[5] Snijder, H. H., van der Aa, R. P., Hofmeyer, H., & van Hove, B. W. E. M. Lateral torsional buckling design imperfections for use in non-linear FEA. Steel Construction: Design and Research, 11(1), 49 – 56, 2018.
[6] Kettler, M., Lichtl, G., Unterweger, H. Experimental tests on bolted steel angles in compression with varying end supports. Journal of Constructional Steel Research, 155, 301 – 315, 2019.
[7] Kettler, M., Taras, A., Unterweger, H. Member capacity of bolted steel angles in compression: Influence of realistic end supports. Journal of Constructional Steel Research. 130, 22 – 35, 2017.
[8] prEN 1993-1-13:2020: Eurocode 3: Design of steel structures – Part 1-13: Steel beams with large web openings, draft, CEN, 2017.

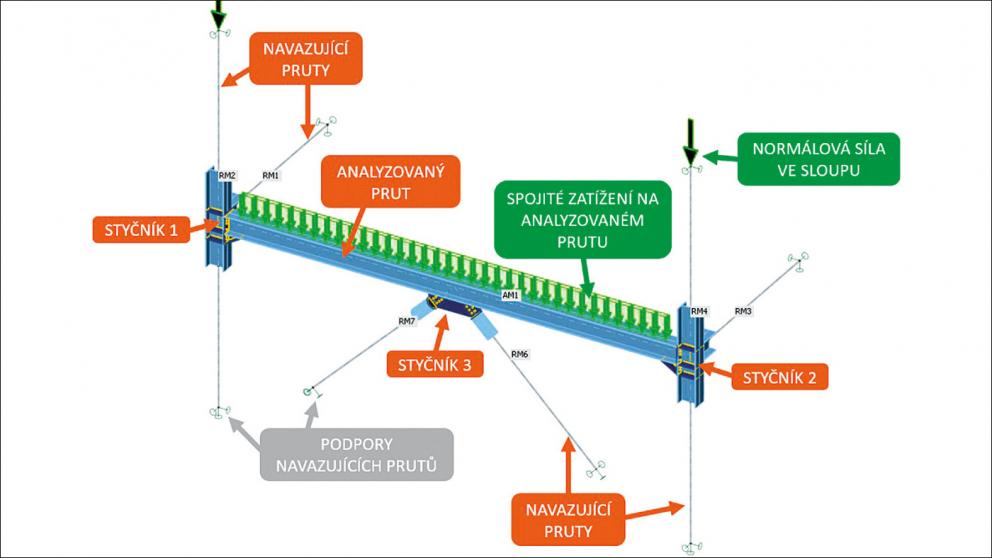 CBFEM model analyzovaného prutu, který je součástí ztuženého rámu
CBFEM model analyzovaného prutu, který je součástí ztuženého rámu