Článek je zaměřen na navrhování styčníků uzavřených průřezů. Krátce popisuje metodu způsobů porušení uvedenou v normě. Tato metoda je použitelná pouze pro vybrané geometrie styčníků a není obecně platná. Tyto nedostatky nahrazuje metoda konečných prvků s komponentami (CBFEM), která je ověřena na rozsahu platnosti normy.
Ocelové uzavřené průřezy jsou stále častěji využívány v nosných konstrukcích pro svou architektonickou čistotu a odolnost proti korozi. Nejčastěji jsou používány v příhradových konstrukcích, na což reagují i normy, které popisují typické styčníky a jejich módy porušení. V praxi to ovšem přináší výrazné omezení. Metoda konečných prvků s komponentami (CBFEM) je obecná a umožňuje spočítat prakticky vše. V tomto článku je popsáno ověření CBFEM na styčnících CHS a SHS průřezů v rozsahu platnosti návrhu normy prEN 1993-1-8:2020 [1].
METODA ZPŮSOBŮ PORUŠENÍ
Styčníky ocelových uzavřených průřezů jsou tradičně posuzovány pomocí metody způsobů porušení (Failure Mode Method – FMM). Tato metoda je zakomponovaná v normě EN 1993-1-8:2005 [1]. Návrh normy prEN 1993-1-8:2020 [2] je doplněn o nové poznatky a vzorce jsou zpřesňovány. FMM je založena na empirických vztazích. Pro určitý tvar styčníku jsou uvažovány určité způsoby porušení. Jejich únosnost je stanovena na základě experimentů a validovaných numerických modelů. Vztahy byly získány proložením výsledků únosnosti nejvhodnější křivkou. Pro tuto metodu je definován rozsah platnosti kvůli omezenému počtu provedených experimentů.
Únosnost styčníků prutů uzavřených průřezů je stanovena pomocí dvou kritérií [1]:
- Dosažení mezního zatížení.
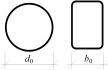
- Dosažení 3% přetvoření průřezu (ε = δ/d0 pro kruhové průřezy, ε = δ/b0 pro hranaté průřezy).
kde δ je deformace průřezu a d0 a b0 jsou vnější rozměry uzavřených průřezů, viz obr. 1.
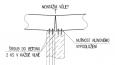
Zejména pro symetrické styčníky (např. tvaru X) namáhané tahem síla roste téměř lineárně, dochází ke stále větší deformaci, dokud nedojde k porušení svarů či tepelně ovlivněných oblastí. Naopak styčníky namáhané tlakem mohou selhat i boulením stěn, které se rozvíjí po dosažení meze kluzu, viz obr. 2.
Validace FMM přípoje plechu na CHS je ukázána na obr. 3. Všechny experimenty uvnitř rozsahu platnosti jsou alespoň 15 % na stranu bezpečnou. V grafech jsou uvedeny také výsledky experimentů mimo rozsah platnosti.
NAVRHOVÁNÍ METODOU KONEČNÝCH PRVKŮ
Numerické modely lze rozdělit na vědecké, které lze označit numerickými experimenty, a na návrhové, které jsou značně jednodušší. Vědecké numerické modely většinou obsahují reziduální napětí a naměřené imperfekce. Pro statickou analýzu styčníků se používá geometricky a materiálově nelineární analýza, která je v současnosti nejpokročilejší.
Component-based finite element method (CBFEM) patří mezi návrhové. Imperfekce ani reziduální napětí nejsou v modelech zahrnuty. Pro většinu typů styčníků postačuje materiálově nelineární analýza (MNA), avšak pro styčníky uzavřených průřezů, kde dochází k poruše boulením, může MNA nadhodnocovat únosnost. Nestačí ani lineární analýza vlastních tvarů ztráty stability (LBA), protože ke ztrátě stability dochází často až po dosažení meze kluzu.
Zde je nutná geometricky nelineární analýza (GMNA), která poskytuje přesnější výsledky. Největší rozdíl mezi únosností stanovenou pomocí GMNA a MNA je u průřezů s velkým poměrem d/t, kde d je vnější rozměr průřezu a t je tloušťka stěny průřezu.
Metoda konečných prvků umožňuje navrhnout libovolný styčník, ale její výsledky musí být ověřené. CBFEM automaticky generuje model a jeho výsledky jsou ověřeny v následující kapitole.
Pro stanovení únosnosti jsou použita dvě kritéria:
- dosažení 5% přetvoření plechů
- dosažení 3% přetvoření průřezu (ε = δ/d0 pro kruhové průřezy, ε = δ/b0 pro hranaté průřezy)
Svary byly navrženy s plnou únosností.
VERIFIKACE
Verifikace je srovnání navrženého modelu s jinou ověřenou metodou, v tomto případě srovnání CBFEM využívající GMNA s metodou způsobů porušení z prEN 1993-1-8:2020 [1]. Styčníky uzavřených průřezů je možné verifikovat ve stejném rozsahu použitelnosti, který platí rovněž pro metodu způsobů porušení. Byly ověřeny rovinné styčníky tvaru T, Y, X a K průřezů CHS a SHS, viz obr. 4 [4].
Důraz byl kladen na zachycení všech způsobů porušení a na obsažení celé škály rozsahu použití.
Studie vykazuje dobrou shodu výsledků určených pomocí CBFEM a metody způsobů porušení, viz tabulka 1. Rovněž způsob porušení se shoduje. Rozdíly mohou být způsobeny odchylkou metody způsobů porušení a experimentů (reálných i numerických) na okrajích rozsahu použitelnosti.
Tab. 1 – Poměr výsledků únosností CBFEM / FMM
| průměr | minimum | maximum | |
| CHS | 97,0% | 86,7% | 112,3% |
| SHS | 93,7% | 86,6% | 107,5% |
| Plech | 100,6% | 95,0% | 106,5% |
ZÁVĚR
Únosnost styčníků uzavřených průřezů je tradičně stanovena metodou způsobů porušení. Vzhledem k tomu, že tato metoda vznikla stanovením vhodné křivky prokládající výsledky experimentů a vědeckých numerických modelů, nabízí se možnost navrhovat styčníky uzavřených průřezů přímo pomocí numerické analýzy. Pro styčníky prutů uzavřených průřezů byla do CBFEM zavedena geometricky a materiálově nelineární analýza, která je schopna postihnout všechny způsoby porušení. CBFEM vykazuje dobrou shodu s postupem v návrhu normy prEN 1993-1-8:2020.
Návrh metodou konečných prvků s komponentami umožňuje výrazně vyšší variabilitu, například posouzení styčníků s vloženými plechy, které nejsou zahrnuty v normě.
Přestože tyto styčníky už nelze přímo verifikovat, lze očekávat, že výsledky jsou rovněž platné, pokud zůstane respektován rozsah platnosti normy – poměr d/t.
Ing. Martin Vild, Ph.D.
Ing. Lubomír Šabatka, CSc.
Ing. Jaromír Kabeláč, PhD.
IDEA StatiCa s. r. o.
prof. Ing. František Wald, CSc.
Ing. Matyáš Kožich,
ČVUT v Praze, Stavební fakulta,
Katedra ocelových a dřevěných konstrukcí
REFERENCE:
[1] prEN 1993-1-8:2020, Eurocode 3, Design of steel structures, Part 1-8, Design of joints, CEN, Brusel, šestý návrh, 2020.
[2] ČSN EN 1993-1-8 ed. 2: Eurokód 3: Navrhování ocelových konstrukcí – Část 1-8: Navrhování styčníků, Praha, UNMZ, 2013.
[3] Wardenier J., Kurobane Y., Packer, J.A., van der Vegte, G.J., Zhao, X.-L. Design guide for circular hollow section (CHS) joints under predominantly static loading, CIDECT, 2008, ISBN 978-3-938817-03-2.
[4] Wald, F. et al. Component-based finite element design of steel connections. Czech Technical University in Prague, 2020, ISBN 978-80-01-06702-4

 Netypický styčník, který není zahrnutý v normě, ale je řešitelný CBFEM
Netypický styčník, který není zahrnutý v normě, ale je řešitelný CBFEM